钟志华 涂荣豹
（南通大学，江苏 南通 226007 南京师范大学，江苏 南京 210097）

  美国教育家J.J.施瓦布（J.J.Schwab）提出的探究性教学理论已经走过近半个世纪的历程，但探究性教学走向实践的进程似乎有些步履蹒跚。怎样让实践更好地接纳探究性教学，我们需要创造出让广大教师易学好用的“快捷式”探究性教学策略。而要构建这样的教学策略，我们不仅需要深入研究探究性教学的本质，同时需要深入研究探究性教学理论在实践中的应用。
  一 精心设计探究性问题：探究教学的起点
  探究性教学始于问题，问题是探究性教学的核心，没有问题便没有探究。对于问题，目前多数人比较赞同A.纽厄尔（A.Newell）与H.A.西蒙（H.A.Simon）的定义：问题表示这样一种问题情境，即个体想做某事，但不能马上知道完成这件事所需采取的一系列行动。每一个问题都包含3种成分：目标，指有关问题结果状态的描述；给定信息，指有关问题初始状态的一系列描述；障碍，指在解决问题的过程中会遇到种种需要解决的因素。问题实际上就是在给定信息与目标之间有某些障碍需要加以克服的情境。然而，并非所有的问题都具有探究价值。什么样的问题才具有探究的价值呢？一般认为，问题探究价值的大小取决于问题的起点与目标之间潜在距离的大小。这两者的潜在距离越大，探究的空间也就越大，就越能激发学生积极思维。换句话说，当两者的潜在距离较小，容易为学生所理解和掌握时，问题就是接受式的；而当两者的潜在距离较大，需要学生努力思考才能解决时，问题就成为探究式的。钟启泉认为，问题的探究性取决于问题的开放性。所谓“开放性”有如下标准：是否能引导学生进行更深入和更高层次的思考？是否能促进学生深入探究重要的知识以及它们之间的联系？是否能引导学生思考超越课堂教学事物的价值和意义？是否建立在学生已有的知识和观念的基础上，促使他们将已有的概念、知识和技能与探究过程联系起来？是否能鼓励和尊重所有的学生参与到探究活动中来？
  探究性问题既有别于人们常说的“原始性问题”，也不同于学科中的问题或习题。“原始性问题”是指自然界及生活、生产、科研中客观存在的、未被加工的问题，也可以称做实际问题。“原始性问题”虽然具有探究价值，但未必适合在课堂上探究，而学科中的问题或习题未必就没有探究价值。探究性问题的本质在于问题的开放性，在于能够充分拓展学生探究的空间。至于问题的形式则没有统一的标准，它既可以来自生活，也可以来自生产实践，甚至还可以直接来自于学科或教材。同时，探究性本身也是一个相对的概念。一方面，一个知识对于不知道结果的人来说可能具有探究价值，而对于已经知道结果的人来说则已无探究价值；另一方面，一个看上去没有探究价值的问题，若换一个角度来看或者进一步深入挖掘又会变得有探究价值。例如，在“圆的认识”的教学中，一位老师在研究了圆的半径与直径的性质后，给学生布置了这样一个任务：找出圆形纸片与黑板上所画圆的圆心。对于这样的问题，学生可能给出多种回答，如：“连接圆上任意两点所成的弦中，直径最长”，“直径将圆分成了相等的两部分”；等等。通过这样的提问，课本上原本普通的问题变成了探究性问题。
  既然问题是探究性教学的起点，那么在进行探究性教学时教师应该善于创设问题情境，善于运用各种方法提出或引导学生提出具有探究价值的问题。如苏格拉底的“反讽”法、美国学者S.布朗（S.Brown ）与 M.沃尔特（M. Walter）提出的“否定假设法” 等都很好地体现了探究性教学思想。所谓“否定假设法”，即如果它不是这样的，那又可能是什么呢？它是通过对原问题的条件和限定进行自由改变产生新问题的方法。
  二 详细编制探究导向图：引导探究实践的罗盘
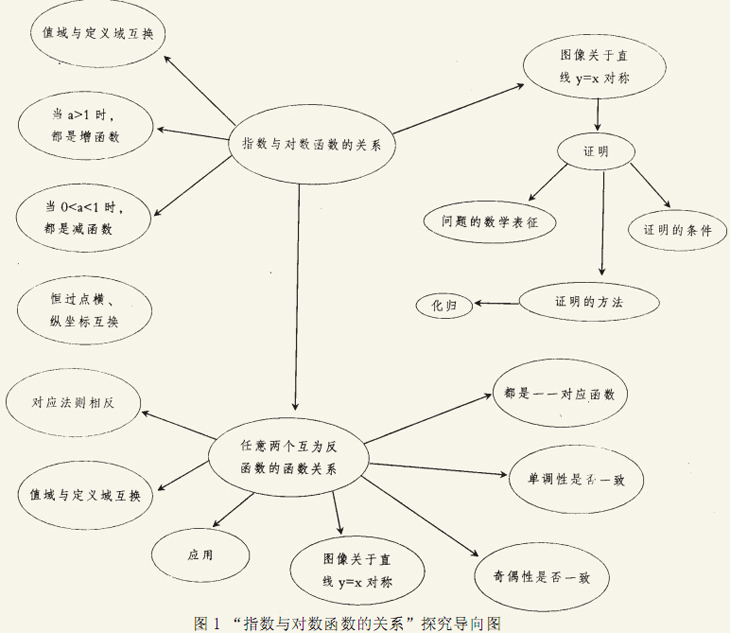
  探究性教学具有预设性，而不是“信手拈来”，这就要求教师在课前对预设问题以及课堂上随时生成的问题预先进行探究，并在此基础上系统地整理和设计这些内容。弗利德曼认为，成功的教学必须使学生掌握正确的和完全的导向系统———运用逻辑形式和规则的活动导向结构。受“概念图”思想的启发，结合Л.М.弗利德曼的“活动导向结构”，钟启泉教授认为，在进行探究性教学之前教师通常应准备好一个提问或者讨论的框架。我们认为，在进行探究性教学时，教师应该在课前对探究的内容、过程以及拟采用的方法进行精心研究的基础上，编制一张关于整个探究过程的知识结构以及探究过程的网络图，简称探究导向图。导向图要详细标明探究的起点是什么？探究的目标有哪些？探究过程经过哪些中间环节？以及如何达到探究的目标？只有这样，才能对学生的探究过程进行准确定位，以便决定下一步探究的方向和选择引导的策略，而不至于在探究过程中过于随意而偏离教学目标。我们可以参考一下南京师范大学附中一位教师的探究导向图，如图1所示。

  当然，探究活动不可能完全按照预先设计的流程按部就班地进行。这是因为，一方面，教师不可能事先预测到探究的所有过程和结果；另一方面，学生也未必完全按照教师事先设计的流程来进行探究。这就需要教师在充分把握探究导向图的基础上，根据学生探究活动的动态变化，采取灵活而恰当的元认知提问来引导学生的探究进程；同时还需要教师有丰富的探究经验和良好的探究直觉，以正确地预判和适时地调整下一步探究的方向，并进而选择恰当的元认知提问来促进探究的顺利展开。
  三 灵活运用元认知提问：促进探究深入的动力
  所谓“元认知提问”，是为了激发元认知活动而使用的提问。元认知提问不直接指向具体问题，其目的在于激发元认知调节，监控认知活动。元认知提问既可以由教师提出，也可以由学生自己提出。元认知提问不同于一般的认知提问，它们的差别主要在于认知提问离具体问题较近甚至有时是直接就具体问题进行提问，而元认知提问则离具体问题较远。但在具体问题中，究竟什么是认知提问、什么是元认知提问，实际上有时很难做出严格的区分。因为认知提问与元认知提问实际上是一个连续的谱。在探究教学中，启发的过程实质上是“由远及近”———从运用较多元认知成分到较少元认知成分直到最后运用认知提问为止的一个连续不断的过程。区分认知提问与元认知提问的最重要标准是看其所激发的思维活动空间的大小。在教学中，常见的元认知提问有：“我们现在应该研究什么？”“你们能提出什么问题？”“怎么研究？”“有哪些研究方法？”“你有什么发现？”“为什么？”“你能解释吗？”“你能证明吗？”“还有其他发现吗？”等等。
  元认知提问在探究性教学中有着十分重要的作用，它既是引导认知活动的路标，又是促进探究深入的动力。这是因为探究既是一个目标导向过程，又是一个自我调节和反思总结过程。探究总是在一系列问题的引导下展开的，离开问题的引导，探究就会迷失方向，也会失去前进的动力。探究学习过程中的每一个环节都离不开元认知指引和发动。目标导向的过程是运用元认知确定探究目标和选择认知策略的过程，探究展开的过程是运用元认知调节、监控探究方向并促进探究前进的过程，反思总结过程则是运用元认知检验探究成功得失的过程。可见，探究学习活动的过程总是伴随着元认知的。因此，教师在探究性教学活动中要有意识地运用元认知提问来促进学生探究活动的持续深入，特别要注意引导学生自己运用元认知来促进探究活动的进行。教师可以引导学生进行“自我提问”式的反思，如“探究沿什么方向前进？”“其成功的可能性有多大？”“所猜想问题的正确程度如何？”等。
  元认知提问既要根据预先设计好的探究导向图来实施，又要根据学生的理解情况以及探究的进程来进行动态调整。只有充分考虑这两个方面，才能提出切实符合学生实际的元认知提问，才有可能充分激发学生的思维活动。至于怎样引导学生运用元认知提问来进行探究性教学，我们可以参考钟启泉教授提出的如下步骤： 1）现在我们正在做什么？ 2）我们有没有了解这个探究主题的大致轮廓？ 3）我们现在掌握了哪些与该主题有关的事实？4）进行这个主题探究的意义是什么？ 5）处理该主题的最好方法是什么？ 6）我们过去是否经历过这样的情境？ 7）我们用这种方法处理是否正确？是否还有其它方法？ 8）我们是否充分了解这类事物？ 9）我们需要知道哪些事实？ 10）我们从哪里可以获得这方面的事实信息？
  为了更好地了解元认知提问在探究教学中的运用，我们来看一个具体的实例。按照上面的探究导向图，这位教师首先提出了问题“你觉得指数与对数函数之间有什么关系？你打算怎么研究？”当学生做出回答后，教师进一步提问“还有其他关系吗？”这时，有学生想到恒过点的横、纵坐标互换，但没有发现图形关于直线y=x对称。于是，教师及时利用几何画板进行直观演示来启发学生：变动a的大小，观察这两个函数的图像之间的什么关系。当学生发现这两个函数的图像关于直线y=x对称时，教师进一步追问“对于你所发现的关系能给出证明吗？”引导学生探索证明的思路和方法。在给出反函数的定义后，教师又立即提出“为什么给它取名为反函数？你觉得这个‘反’到底反在什么地方？”这样一个核心问题，再一次激起学生强烈的探究欲望。在学生回答了“对应法则互反，定义域与值域互换”以后，教师又提出一连串逐次递进的元认知问题：“是不是所有的函数都有反函数？”“到底什么样的函数具有反函数？”“原函数与反函数之间到底有什么关系？”再一次把探究活动推向高潮。当学生总结上面的研究以为探究快要结束之时，教师进一步追问：“在一般情况下，互为反函数的两个函数之间的性质还有什么关系？”激发起学生对函数的单调性、奇偶性等进行更全面、更深入的考察，引发学生开展讨论，使学生的思维达到高潮。在下课之前，教师又适时地提出了一个统领全课的问题：“请大家反思一下，你觉得学了反函数有什么好处？”这既起到了画龙点睛的作用，又让人回味无穷。